Ensemble Learning and Random Forests

Introduction

Let’s start with a game.

Exercise

In groups of 6 to 8 people, estimate first individually and then collect your answers on the following questions:

A regression question: What is the age of the instructor?

A Physics question: Which fundamental interaction is the strongest: Electromagnetism, Weak Force, Strong Force or Gravity?

A question of your choice (but with an answer available on the web)

For the regression, compute the average of your answers.
For the classification, count your votes and pick the class collecting most votes.
What do you notice?

We attribute to Aristotle the old adage “the whole is greater than the sum of its parts.” The exercise above is an example of the so-called “wisdom of the crowd,” where the collective brings a better answer than the individual guesses. Such a technique of getting a prediction from aggregating a collection of predictors is called Ensemble Learning.

Definitions

Definition 44

An Ensemble Learning is a technique consisting of aggregating the predictions of an Ensemble, i.e. a group of predictors.

An Ensemble Learning algorithm is called an Ensemble method.

The more diverse the predictors within the ensemble, the better to obtain an accurate final prediction. The fascinating part: the global prediction not only outperforms each individual learners, but the predictors do not have to be that good for this to work. We refer to a not-so-good predictor as a weak learner. Once combined, the ensemble method can generate higher accuracy in the final prediction: it has become a strong learner.

How are the individual results from the predictors combined?

For regression, taking the average of the predicted values is the most natural way.

For classification, the aggregation is done either through a counting of votes, i.e. which class receives the most predictions (each predictor produces one vote). Or via probability if the predictors provide this information along with the predicted class: the prediction associated with the highest probability wins.

Definition 45

When the combined result of an Ensemble method is done by…

… counting the class that gets the most votes among the predictors, i.e. a majority-vote aggregation, we call this is a hard voting classifier.

… choosing the class that comes with the highest associated probability (provided the information is available): this is a soft voting classifier.

The hard voting could appear advantageous, it is however impossible to know how confident each vote is, whereas the soft voting benefit from that information. Soft voting thus performs generally better.

There is another concept important in ensemble learning: bagging.

Remember that in ensemble learning, diversity is key. Yet it can be impractical to train very diverse learners, each having their own specificities and drawbacks to pay attention to. An alternative approach is to deal only with one algorithm but increase the diversity in the dataset. Like shuffling a deck of cards, bagging involves training predictors on randomized subsets of the dataset.

Definition 46

Bagging, short for bootstrap aggregating, is a method in ensemble learning consisting of resampling multiple times the dataset with replacement, i.e. the procedure can select a data point more than once in a resampled dataset.

Pasting refers to a similar protocol but without replacement (no repeated data points).

Recall the instability characteristic to decision trees. By varying the dataset multiple times, such instabilities are averaged out by all other predictions. In the end, even if each predictor is more biased (due to a given sampling), the aggregated results reduce both bias and variance.

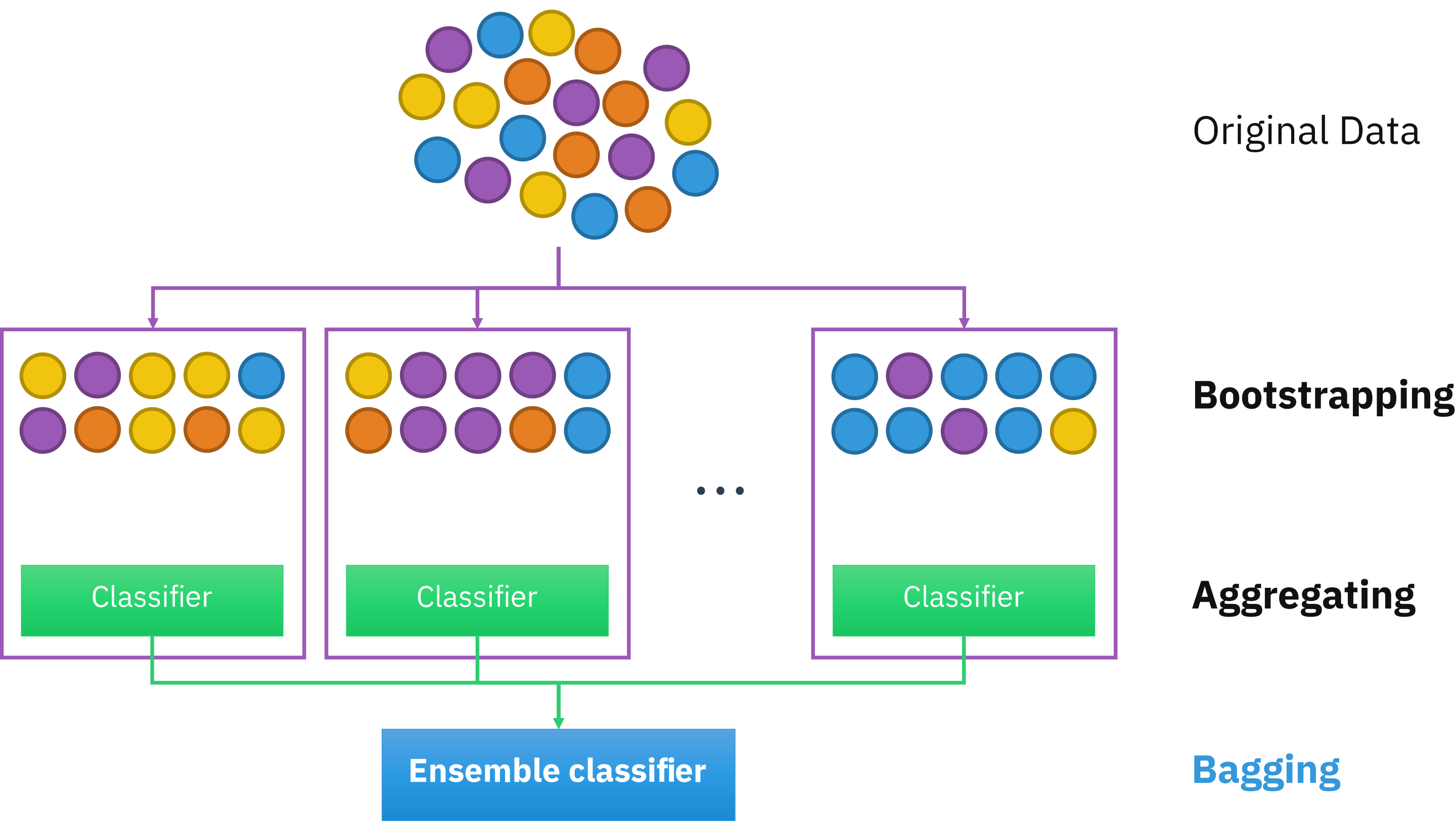
Fig. 34 . Visual of bootstrap aggregating or bagging.
_{Source: Wikipedia}

So far we have said nothing from the type of predictors. Let’s see a particular example of ensemble method whose predictors are decision trees. The name follows naturally: it’s a forest.

Random Forest

Presentation

Definition 47

A random forest is an ensemble learning made of solely decision trees.

Class prediction is done by selecting the class obtaining the most votes among all decision trees’ predictions.

Random forest classifiers are implemented in Scikit-Learn from the ensemble library. Here is a minimal code:

from sklearn.ensemble import RandomForestClassifier

rnd_clf = RandomForestClassifier(n_estimators=500, max_leaf_nodes=16, n_jobs=-1)
rnd_clf.fit(X_train, y_train)

y_pred_rf = rnd_clf.predict(X_test)

Only four lines. But there are obviously much more lines of code ‘backstage’ behind those calls. It’s important to understand what these methods do as well as their arguments.

• n_estimators refers to the number of trees in the forest

• max_leaf_nodes is a hyperparameter regularizing each tree

• n_jobs tells how many CPU cores to use (-1 tells Scikit-Learn to use all cores available)

The Random Forest inherits all hyperparameters of the decision trees. There are other hyperparameters proper to Random Forest classifiers, for instance activating the bagging bootstrap=True with max_samples controlling the sample size of each subset.
More on Scikit-Learn RandomForest page.

Advantages

Random forests are popular as they present numerous qualities:

• their results are among the most accurate compared with other machine learning algorithms

• they are less likely to overfit the data

• they run quickly even with a large dataset

• they require fewer data to train

• they are easy to interpret

• they can be scaled using parallel computing (cores)

• they can rank the features by their relative importance

More about the last point: random forest classifiers not only classify the data, they can also measure the relative effect, or importance, each feature has with respect to the others. This is very handy while designing a machine learning algorithm to see which features matter. If for instance there are too many features, a random forest can help reduce this number while not removing key features. Scikit-Learn computes the feature importance automatically after training. It is expressed as a score, ranging from zero (useless feature) to 1 (most important). Here is a snippet showing how to access the feature importance scores:

# Dataset loading (not written): X and y dataframes

rnd_clf = RandomForestClassifier(n_estimators=500, n_jobs=-1)
rnd_clf.fit(X, y)

for name, score in zip(X.columns, rnd_clf.feature_importances_)
    print(name, score)

This will output something in the like:

    x1  0.11323
    x2  0.54530
    x3  0.05961
    ...

The sum of all feature importance is 1.

We have seen the advantage of decision trees working together in a beautiful forest to produce low variance predictions. Let’s go one step further: the boosting.