Limitations#

Cutting down on overfitting#

Decision trees are choosing the cut values solely on the available dataset. If let unconstrain, they will continue their way cutting through the data noise, ineluctably leading to overfitting. The way to regularize them is done through the hyperparameters, restricting their freedom:

  • maximum depth is stopping the algorithm after the node ‘depth - 1’ (as the starting node is zero)

  • minimum sample split is the minimum number of samples a node must have before it can be split

  • minimum sample leaf restricts the number of samples within a leaf, preventing an over-segmentation of the data into small square ‘islands’ with very few data samples in them

  • maximum leaf nodes is an upper bound on the amount of leaves (final nodes)

Exercise

How to tweak (increase of decrease) the hyperparameters in order to relevantly perform a regularization?

Check your answers

Hyperparameters with minimum in their name regularize the tree when increased, while those with maximum in their name regularize it when decreased.

Orthogonal cuts#

As the decision trees work with threshold values, the boundaries are always perpendicular to an axis. This works well if the data is ‘by chance’ aligned with the axes. This ‘feature’ makes decision trees sensitive to rotation. If we rotate the dataset used in the example above, we can see it changes decision boundaries:

angle = np.pi / 180 * 20
rotation_matrix = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]])
Xr = X.dot(rotation_matrix)

tree_clf_r = DecisionTreeClassifier(random_state=42)
tree_clf_r.fit(Xr, y)

plot_decision_boundary(tree_clf_r, Xr, y, axes=[0.5, 7.5, -1.0, 1])
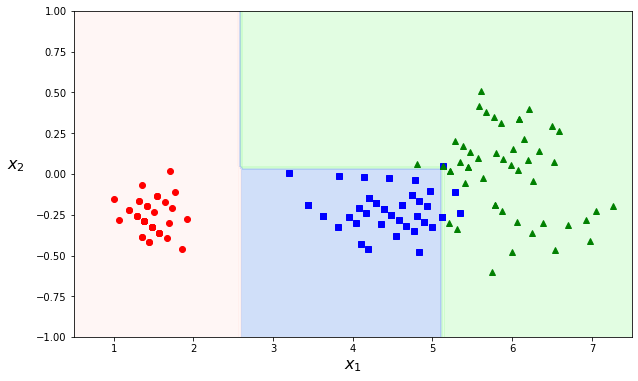
../_images/BDTs_demo_18_0.png

Instability#

Not only rotated data samples, decision trees can also drastically change with only minimal modification in the data. Removing one data point in the dataset above can lead to very different decision boundaries:

../_images/BDTs_demo_21_0.png

Instability will change future predictions and is quite a bad feature (bug) from a machine learning algorithm. How to circumvent this intrinsic instability? This is what we will cover in the next section!