What are Decision Trees?

Introduction

Without knowing, you may have already been implementing a ‘decision tree’ process while making a choice in your life. For instance, which cereal box to buy at the store. There are so many brands and options (understand classes) that it can be overwhelming. Here is a tree-like reasoning example:

• Does it have more than three types of flakes? No? Too boring. Yes? Let’s move on:

• Is a portion bigger or lower than 300 calories? Bigger? It’s not healthy, let’s go lower and see the next parameter:

• Is it crunchy? If yes, I take that one!

Your decision protocol followed a tree process starting with a node (a decision to make), then evaluating a condition on a feature (number of flake type, calorie density, crunchiness factor) and, depending on the answer, another node evaluates another input feature. Such a decision-making process can be visualized like a tree whose branches are the different outcomes and leaves the final choices:

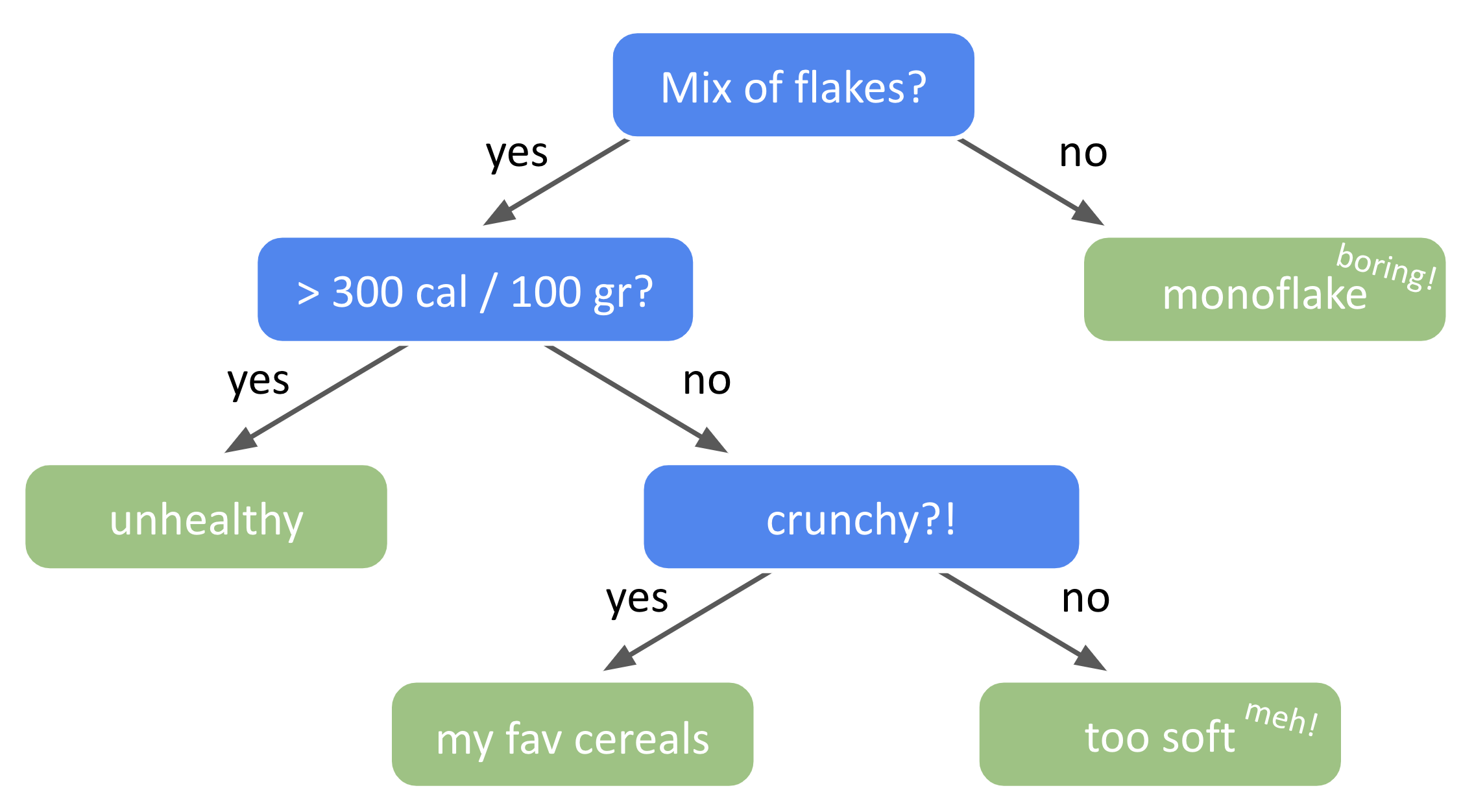
Fig. 25 . An example of decision tree for choosing cereals.
_{Image by the author}

Decision trees belong to the family of machine learning algorithms for both classification and regression (we will focus on classification here).

Definitions

Definition 44

A decision tree is a flowchart mapping a decision making process. It is organized into nodes, branches and leaves.

Definition 45

A tree consists of three types of nodes:

• Root node: The start of the decision process is the first test performed on the whole dataset.

• Internal nodes: A “condition box” evaluating subset of the dataset on a given feature. The test has two possible outcomes: true or false.

• Leaf nodes or terminal nodes: Nodes that do not split further, indicating – most of the time – the final classification of data points ‘landing’ in them.

The outcomes of that evaluation (either boolean or numerical) is divided into branches, or edges. Each branch supports one outcome (usually True/False) on the condition from the previous node.

A particular case of a decision tree, reduced to its bare minimum — just a single split — is called a decision stump.

Definition 46

A decision stump is a one-level decision tree. It has one root node evaluating only one input feature and the two resulting branches immediately connect to two terminal nodes, i.e. leaves.

Example

Let’s illustrate the terminology with an example. Let’s have a dataset with two variables as input features, \(x_1\) and \(x_2\).

    from sklearn.tree import DecisionTreeClassifier

    tree_clf = DecisionTreeClassifier(max_depth = 2)
    tree_clf.fit(X, y)

The code has been shortened for clarity, see the notebook on trees for completeness.

To visualize the work of the decision tree classifier, the graphviz library creates an automated flowchart:

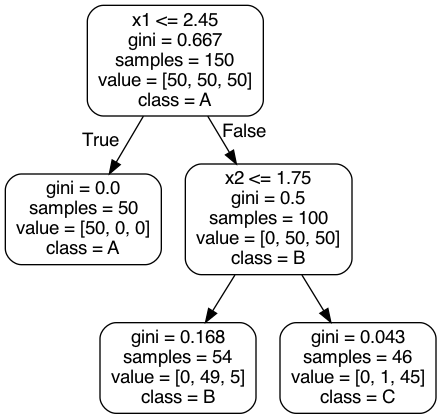
Fig. 26 . Example of a Decision Tree drawn from sklearn pre-loaded dataset iris. The root node is at the top, at depth zero. The tree stops at depth = 2 (final leaves).

Such a flowchart above tells how future predictions are made. Predicting the class of a new data point (\(x_1^\text{new}\), \(x_2^\text{new}\)), one simply follows the ‘route’ of the tree starting from the root node (on top) and ‘answering’ the conditions. Is \(x_1\) lower than 2.45? Yes, go to the left (and it corresponds to predicted class A). If not, go to the next node evaluating \(x_2\) feature, etc.

The predictions can be visualized on a 2D scatter plot. The threshold values are the decision boundaries (see Definition 17 in section What is the Sigmoid Function?) and are materialized by either vertical or horizontal cuts. Instead of a straight line or polynomials fit, a decision tree rather makes an orthogonal segmentation of the phase space.

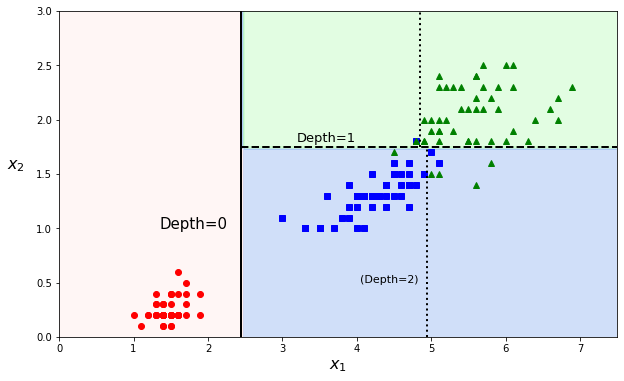
The first node at depth 0 creates a first decision boundary, splitting the dataset into two parts (and luckily isolating class A in a pure subset). The second cut is at depth 1. As the tree was set to a max depth of 2, the splitting stops at depth 1 (as we start from zero). But it is possible to continue further with a max depth of 3 and the decision boundaries (several for each branch) would be the dotted vertical lines.

We could see with an example and illustrative graphs how the decision tree splits the datasets. But how are these splits calculated? Why did the classifier chose the cut values \(x_1\) = 2.45 and \(x_2\) = 1.75? This is what we will cover in the following section.