Motivations

Let’s suppose we have a classification challenge looking like this:

Reminder: in linear and logistic regression, we took as hypothesis function a linear combination of the features with the \(\theta\) parameters: \(h_\theta(x^{(i)}) = \sum_{j=0}^n \theta_j x^{(i)}_j = \theta \cdot x^{(i)}\)

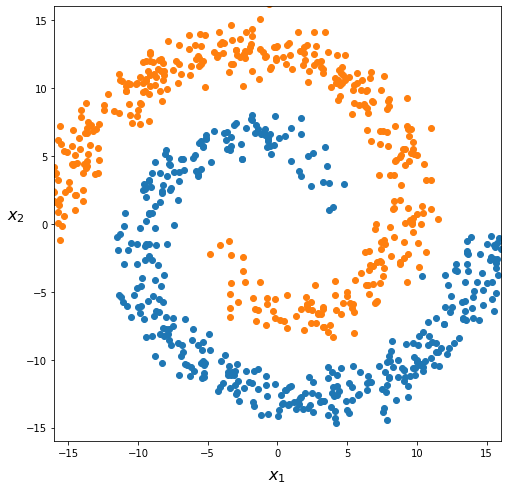
What can be a good hypothesis function? Linearity will not work here, at all. So we will have to include higher degree polynomial terms in our hypothesis function. This would look like:

\[h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_1 x_2 + \theta_4 x_1^2 x_2 + \theta_5 x_1^3 x_2 + \theta_6 x_1 x_2^2 + \cdots \]

If we include lots of polynomials, the hypothesis functions would eventually fit complex data patterns. But there are issues here.

First: to which degree of complexity one should go? Moreover, which polynomials would be more useful to efficiently discriminate between the different classes? We can’t know this in advance (and the dataset above has only two input features so we can see a 2D representation, in real life it is not possible to picture in one graph a dataset with more input features).

Second: with \(n\) input features \(x_1, x_2, \cdots, x_n\), adding quadratic terms will grow the amount of terms in \(h_\theta(x)\) as \(\approx \frac{n^2}{2}\). So with 10 input features we will have 50 quadratic terms. With \(n=100\), we reach \(5000\) of terms! And we would not model complex patterns like the one above. Cubic combinations (\(x_1^3, x_1^2 x_2, x_1 x_2^2, \cdots \)) would add \(\mathcal{O}(n^3)\) new terms… This would become impracticable, likely overfit the data, and will definitely be too computationally intensive.

We will turn to Artificial Neural Networks (ANN or NN for short).

Definition 50

An Artificial Neural Network is a Machine Learning Model inspired by the networks of biological neurons in animal brains.

While the computation in each artificial neuron is simple, the interconnections of the network allow for complex patterns to be modelled.

We will define in the next section important terminology - a lot will be borrowed from what we saw in linear and logistic regression.