Learning Rate

The learning rate decides on the degree of parameter update. The learning rate \(\alpha\) is a hyperparameter intervening in the calculation of the step size at which the parameters will be incremented or decremented.

Learning Rate and Convergence

The learning rate is not directly setting the step size. It is a coefficient. With a fixed \(\alpha\), the gradient descent can converge as the steps will become smaller and smaller due to the fact that the derivatives \(\frac{\partial }{\partial \theta_j} J(\theta)\) will get smaller (in absolute value) as much as we approach the minimum:

Recall that the step size is given by \(-\alpha \frac{d}{d \theta} J(\theta) = -\alpha \times\) slope. Here the magnitude of the slope is decreasing at each iteration. Eventually, \(\frac{d}{d \theta} J(\theta) \rightarrow 0\) so \(\theta' = \theta - \alpha \times 0 \rightarrow \theta \).

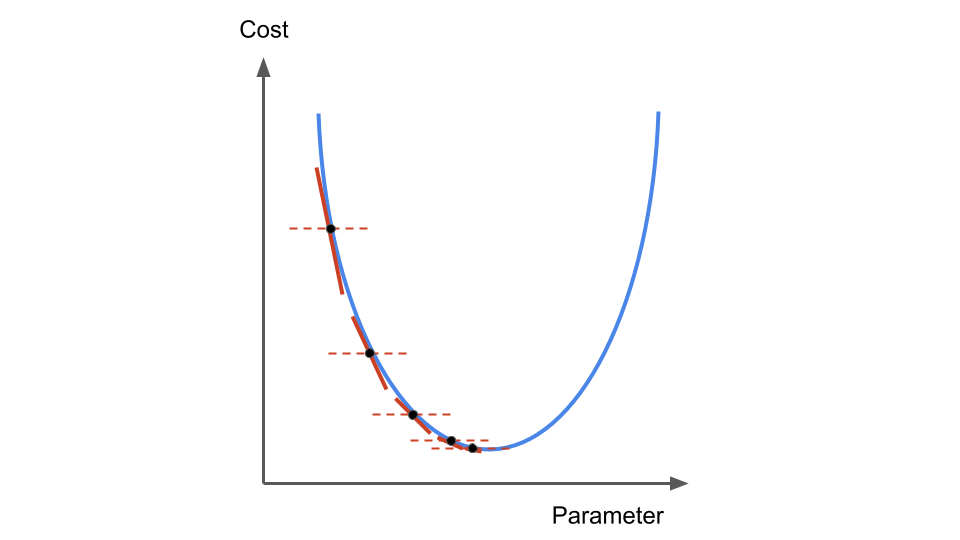
Fig. 15 . The step size is reduced at the next iteration of the gradient descent,
even if \(\alpha\) remains constant. _{Image from the author}

Learning Rate and Divergence

A learning rate too big will generate an updated parameter on the other side of the slope.
Two cases:

• The zig-zag: if the next parameter \(\theta'\) is at a smaller distance to the \(\theta^{\min J}\) minimizing the cost function (\( | \theta' - \theta^{\min J} | < | \theta - \theta^{\min J} |\)), the gradient descent will generate parameters oscillating on each side of the slope until convergence. It will converge, but it will require a lot more steps.

• Divergence: if the next paremeter is at a greater distance than the \(\theta^{\min J}\) minimizing the cost function (\( | \theta' - \theta^{\min J} | > | \theta - \theta^{\min J} |\)), the gradient descent will produce new parameters further and further away, escaping the parabola! It will diverge. We want to avoid this.

The divergence is illustrated on the right in the figure below:

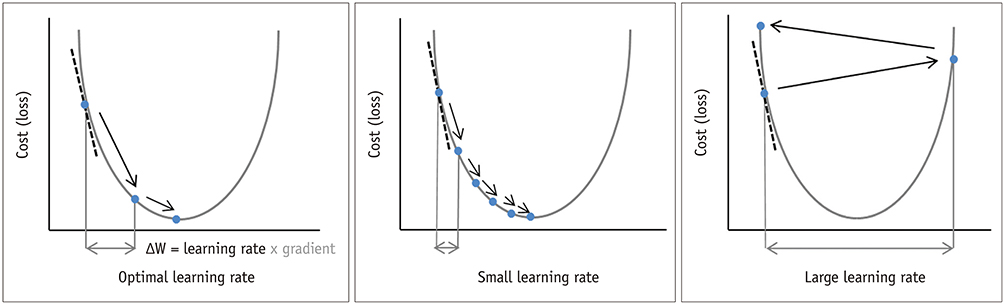
Fig. 16 . The learning rate determines the step at which the parameters will be updated (left). Small enough: the gradient descent will converge (middle). If too large, the overshoot can lead to a diverging gradient, no more “descending” towards the minimum (right). _{Image from kjronline.org}

Summary

• The learning rate \(\alpha\) is a hyperparameter intervening in the calculation of the step size at which the parameters will be incremented or decremented.

• The step size varies even with a constant \(\alpha\) as it is multiplied by the slope, i.e. the derivatives of the cost function.

• A small learning rate is safe as it likely leads to convergence, yet too small values will necessitates a high number of epochs.

• A large learning rate can make the next update of parameters overshoot the minimum of the cost function and lead to either

  • an oscillating trajectory: the algorithm converges yet more iterations are needed

  • a diverging path: the gradient descent fails to converge

Question

How to choose the best value for the learning rate?

We will discuss your guesses. Then the next section will give you the tricks!